Valor absoluto e inecuaciones con valor absoluto
Valor absoluto e inecuaciones con valor absoluto
El valor absoluto de un número a, representado como |a|, es su valor numérico (con signo positivo).
Por ejemplo,
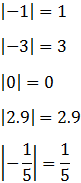
1. Función valor absoluto
Matemáticamente, el valor absoluto es una función (de una variable) de los reales en los reales:
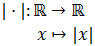
y se define como una función a trozos:
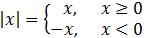
Esta función es continua en los reales y derivable en
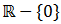
La gráfica de la función es:
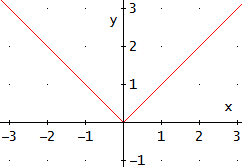
Notemos que en los reales negativos la gráfica es la de y = - x y en los positivos es la de y = x.
2. Propiedades
-
El valor absoluto siempre es mayor o igual que 0, siendo 0 sólo cuando su argumento es 0:
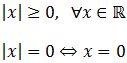
-
El valor absoluto de un producto es el producto de los valores absolutos de los factores:
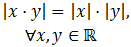
-
Valor absoluto de la suma:
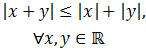
-
Propiedad importante: si tenemos la desigualdad (menor o igual)
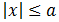
podemos escribir
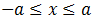
que es lo mismo que decir
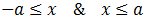
(tienen que cumplirse ambas relaciones).
Dicho en forma de intervalos:
![-x en el intervalo [-a,a] valor absoluto e inecuaciones con valores absolutos](https://www.matesfacil.com/BAC/absoluto/absT-11.png)
Si la desigualdad es (mayor o igual)
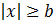
podemos escribir
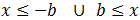
(es una unión: tiene que cumplirse una de las dos).
Dicho en forma de intervalos:
![x en el intervalo ]-infinito, -b] unión [b,+infinito[ valor absoluto e inecuaciones con valores absolutos](https://www.matesfacil.com/BAC/absoluto/absT-14.png)
3. Inecuaciones con valor absoluto
Inecuación 1
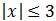
Escribimos la inecuación como
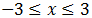
Por tanto, la solución es
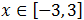
Inecuación 2
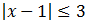
Podemos escribir la inecuación como
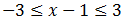
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:
Sumamos 1:
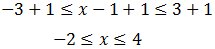
O bien, separar ambas inecuaciones y resolverlas por separado:
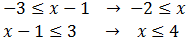
De ambas formas obtenemos la misma solución:
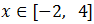
Inecuación 3
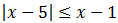
Escribimos la inecuación como:
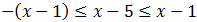
Vamos a trabajar primero con las dos inecuaciones al mismo tiempo:
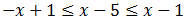
Sumamos 5:
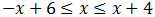
Sumamos x:
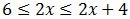
Ahora tenemos que separarlas para obtener la solución:
Por un lado:
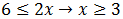
Por otro:
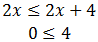
En esta segunda inecuación hemos obtenido una relación que siempre se cumple. Luego no nos aporta restricciones a la solución.
Por tanto, la solución es
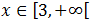
Más información:


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


