Teorema de Pitágoras: Aplicaciones

Jose Llopis
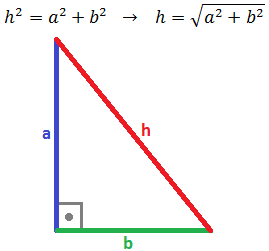
public://teorema-pitagoras.png
Área de conocimiento
Contexto educativo
1625 Visitas
Compartir

logo matesfacil

1. El teorema de Pitágoras

Dado un triángulo rectángulo de catetos a y b e hipotenusa h (el lado opuesto al ángulo recto). Entonces,

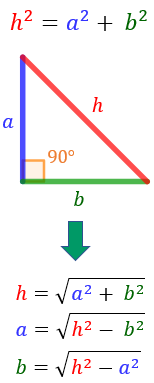
teorema de Pitágoras

Recordemos que:

  1. el triángulo es rectángulo porque tiene un ángulo recto, es decir, un ángulo de 90 grados ó π / 2 radianes.
  2. la hipotenusa es el lado opuesto al ángulo recto

Nota: h siempre es mayor que los dos catetos, es decir, h > a y h > b.

El teorema de Pitágoras es uno de los resultados más conocidos de las matemáticas y también uno de los más antiguos. Existen cientos de demostraciones de este resultado.

2. Ejemplos de Aplicación 

 

2. 1. Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm.

Los lados son

a=3cm , b=4cm

Aplicando el teorema de Pitágoras,

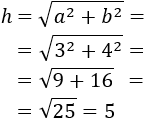
Por tanto, la hipotenusa mide 5cm.

 

2. 2. Calcular la altura del siguiente triángulo sabiendo que sus lados valen 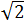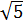raíz cuadrada de 2, raíz cuadrada de 5 y su base 3.

Para poder calcular la altura del triángulo, a, tenemos que dividirlo en dos triángulos rectángulos (para poder aplicar el teorema de Pitágoras).

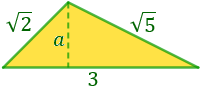
Los dos triángulos son los siguientes:

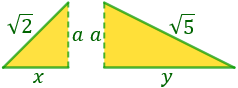
La base del triángulo (que vale 3) se divide en dos (la base de cada triángulo). No sabemos cuánto vale cada base, pero sí que sabemos que

x+y=3

Aplicamos Pitágoras al primer triángulo y obtenemos la ecuación:

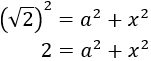
Notemos que no conocemos ninguno de los dos catetos.

Procediendo del mismo modo para el otro triángulo, obtenemos

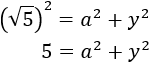
Es decir, tenemos las siguientes ecuaciones:

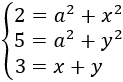
Podemos aislar la y en la tercera ecuación, obteniendo

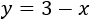
En la segunda ecuación tenemos una y, que sabemos que es 3 - x, así que sustituimos en ella:

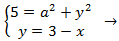
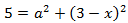
Como tenemos una resta al cuadrado, aplicamos la fórmula del binomio de Newton, que recordamos que es

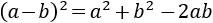
binomio de Newton

Por tanto,

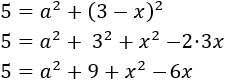
Ahora despejamos a^2

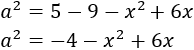
Recordemos que también teníamos la ecuación

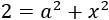
Despejamos también en ella a^2

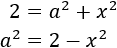
Es decir, las dos ecuaciones que tenemos son

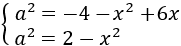
Y como a^2 = a^2, podemos igualar ambas expresiones obteniendo una ecuación de primer grado

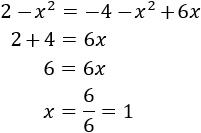
Sabiendo el valor de x podemos obtener el de y

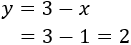
Ya sabemos cuánto vale cada base y podemos ahora calcular la altura.

La primera de las ecuaciones era

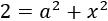
Como sabemos que x = 1 tenemos que

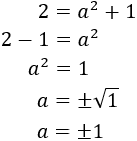
Y como a es la altura, no puede ser negativa. Por tanto, la altura del triángulo es a = 1.

 

3. Más información:

  1. Problemas y Test de Pitágoras
  2. Problemas de Pitágoras
  3. Triángulos (clasificación)
  4. Foro de ayuda
  5. Teorema de Pitàgores
  6. Pythagorean Theorem
  7. Ejercicios interactivos
  8. Ecuaciones Resueltas

Ecuaciones Resueltas:

Otros: